Vektor pada 3 Dimensi

Vektor di R^3

Vektor yang berada pada ruang tiga dimensi (x, y, z).jarak antara dua titik vektor dalam 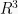 dapat diketahui dengan pengembangan rumus phytagoras. Jika titik  dan titik 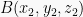maka jarak AB adalah:

Atau jika 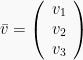, maka

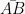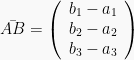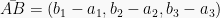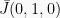Vektor  dapat dinyatakan dalam dua bentuk, yaitu dalam kolom  atau dalam baris . Vektor juga dapat disajikan sebagai kombinasi linier dari vektor basis  dan  dan 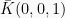 berikut:

Operasi Vektor di R^3

Operasi vektor di 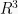 secara umum, memiliki konsep yang sama dengan operasi vektor di  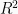dalam penjumlahan, pengurangan, maupun perkalian.

Penjumlahan dan pengurangan vektor di R^3

Penjumlahan dan pengurangan vektor di 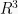 sama dengan vektor di  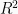yaitu:

Dan

Perkalian vektor di R^3 dengan skalar

Jika  adalah vektor dan k adalah skalar. Maka perkalian vektor:

Hasil kali skalar dua vektor

Selain rumus di 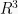, ada rumus lain dalam hasil kali skalar dua vektor. Jika  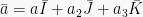dan  maka 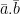 adalah:

Proyeksi Orthogonal vektor

Jika vektor 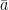 diproyeksikan ke vektor  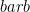dan diberi nama  seperti gambar dibawah:

Diketahui:

Sehingga:

 atau 

Untuk mendapat vektornya:

Contoh Soal Vektor dan Pembahasan

Contoh Soal 1

Diketahui titik A(2,4,6), titik B(6,6,2), dan titik C(p,q,-6). Jika titik A, B, dan C segaris maka tentukan nilai p+q.

Pembahasan 1:

Jika titik-titik A, B, dan C segaris maka vektor 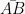 dan vektor  bisa searah atau berlainan arah. Sehingga akan ada bilangan m yang merupakan sebuah kelipatan dan membentuk persamaan

• 

Jika B berada diantara titik A dan C, diperoleh:

• 

sehingga:

Maka kelipatan m dalam persamaan:

Diperoleh:

• 
  
• 
  

disimpulkan:

p+q=10+14=24

Contoh Soal 2

Jika diketahui vektor pada titik A dan titik B dan vektor pada titik C yang berada diantara garis Ab seperti gambar dibawah. Tentukan persamaan vektor C.

Pembahasan 2:

Dari gambar dapat diketahui bahwa:

•  sehingga 
• 

Sehingga:

Contoh Soal 3

Misalkan vektor 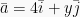 dan vektor . Jika panjang proyeksi vektor 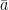a ̅ pada 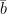 adalah 4. Maka tentukan nilai y.

Pembahasan 3:

Diketahui:

• 
• 

Maka:

12=8+2y

y=2