Bank Soal Matematika

1.Topik : Eksponen

Bentuk sederhana dari adalah….

Kunci : A

Pembahasan :

2. Topik : Eksponen

Nilai x dari persamaan   adalah ….

1. 2
2. 4
3. 6
4. 10
5. 16

Jawaban : E

Pembahasan :

Bilangan berpangkat di soal adalah bentuk permasalahan bilangan berpangkat pecahan, sehingga cara penyelesaiannya sebagai berikut :

3.Topik : Eksponen

Fungsi eksponensial dari grafik di bawah ini adalah ….

1. f(x)=32x
2. f(x)=3x
3. f(x)=3-x
4. f(x)=2x
5. f(x)=2-x

Jawaban: B

Pembahasan

Pada grafik di atas dapat dilihat melalui dua titik, yaitu (0,1) dan (1,3). Untuk mendapatkan fungsi eksponensial tersebut, kita harus mensubstitusikan kedua titik yang ada ke dalam persamaan fungsi eksponensial secara umum f(x)=b × ax untuk mencari nilai a dan b, sehingga:

Untuk titik (0,1) didapat f(x)=b × ax

1=b × a0

1=b × 1

b=1

Untuk titik (1,3) didapat f(x)=b × ax=1 × ax=ax (masukkan nilai b = 1)

f(x)=ax

3=a1

3=a

Maka, fungsi eksponensial dari grafik tersebut adalah

f(x) = b × ax

f(x) =1 × 3x

f(x) =3x

4.Topik : Bilangan bentuk akar

Bentuk sederhana dari bentuk akar  adalah….

Jawaban : A

Pembahasan :

5.Topik : Bilangan Bentuk Akar

Urutan bilangan   dari yang terkecil hingga yang terbesar adalah ….

A.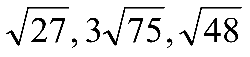 

B.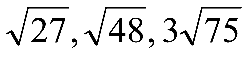 

C.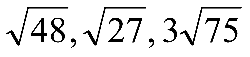 

D. 

E.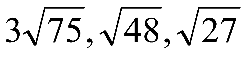 

Jawaban: B

Pembahasan:

Maka urutan dari yang terkecil ke yang terbesar adalah 

6.Topik : Logaritma

Hasil dari adalah ….

1. 1
2. 2
3. 3
4. 4
5. 5

Jawaban: A

Pembahasan:

7.Topik : Logaritma

Jika diketahui  Maka nilai dari adalah ….

Jawaban: A

Pembahasan:

8.Topik : Persamaan dan Pertidaksamaan Linier

Nilai x dari persamaan linier  7x+23=4x-1 adalah ….

1. -3
2. -1
3. 0
4. 1
5. 3

Jawaban: D

Pembahasan

7x+23=4x-1

7x+2=3(4x-1)

7x+2=12x-3

7x-12x=-3-2

-5x=-5

9.Topik : Fungsi Kuadrat

Persamaan kuadrat yang melalui titik-titik (-3, -1), (-1, -5), dan (2, 4) adalah….

1. y = x2 + 2x – 4
2. y = x2 – 3x – 4
3. y = 2x2 + 2x + 5
4. y = x2 – 3x + 5
5. y = 2x2 + 2x – 5

Jawaban : A

Pembahasan :

Persamaan parabola : y = ax2 + bx + c

Titik (-3, -1) → 9a – 3b + c = -1 ………….(1)

Titik (-1, -5) → a – b + c = -5 …………….(2)

Titik (2, 4)    → 4a + 2b + c = 4 …………..(3)

Eliminasi pers. (1) dan (2) :

9a – 3b + c = -1

 a – b + c   = -5   –

8a – 2b = 4

4a – b = 2 ………………..(4)

eliminasi persamaan (2) dan (3) :

 a – b + c   = -5

4a + 2b + c = 4    –

-3a – 3b = -9

a + b = 3 ………………..(5)

eliminasikan persamaan (4) dan (5) :

4a – b = 2

a + b = 3  +

5a = 5

a = 1

subsitusikan ke persamaan (5) :

a + b = 3

1 + b = 3

b = 2

subsitusikan ke persamaan (3)

4a + 2b + c = 4

4(1) + 2(2) + c = 4

c = -4

Persamaan kuadratnya : y = x2 + 2x – 4

10.Topik : Sistem Persamaan Linier Kuadrat Dua Variabel (SPLKDV)

Himpunan penyelesaian antara kurva x2+y2-2xy-1=0 dan garis  x-2y-2=0 adalah ….

1. (0, 1) dan (4,-3)
2. (0, 1) dan (-4,-3)
3. (0, -1) dan (4,3)
4. (0, -1) dan (-4,-3)
5. (0, -1) dan (-4,3)

Jawaban: D

Pembahasan:

x – 2y – 2 = 0 → x = 2y + 2

Substitusi x=2y+2 ke persamaan kurva x2+y2-2xy-1=0

(2y+2)2+y2-2(2y+2)(y)-1=0

4y2+8y+4+y2-4y2-4y-1=0

y2+4y+3=0

(y+1)(y+3)=0

y1=-1 dan y2=-3

Substitusikan nilai y yang telah didapatkan ke salah satu persamaan:

Untuk y1=-1, x1=2(-1)+2=0

Untuk y2=-3, x2=2(-3)+2=-4

Maka, penyelesaian sistem persamannya adalah (0, -1) dan (-4,-3).